Razão e Proporção

Razão

Dados dois números reais quaisquer: a e b, sendo que b é diferente de zero, dizemos que a razão de a por b é a divisão de a por b ou seja a/b.  Chamamos "a" de antecedente e "b" de consequente.

Exemplo: 8/12 (lê-se: 8 está para 12), 8 é o antecedente e 12 é o consequente.

Proporção

É uma igualdade entre duas razões

Exemplo1

a/b = c/d ----> a.d = b.c 

Exemplo2

2/5 = 4/10 --->2.10 = 5.4 --->20 = 20 (verdadeiro)

Propriedades das Proporções Equivalentes

1.  O produto dos meios é sempre igual ao produto dos extremos (comprovado acima);

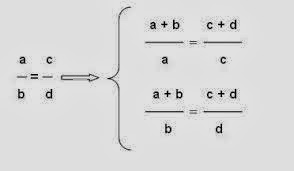
2.  a/b=c/d ---> (a+b)/a = (c+d)/c ou  (a+b)/b = (c+d)/d;

3.  a/b=c/d ---> (a-b)/a = (c-d)/c  ou  ---> (a-b)/b = (c-d)/d;

4. Em toda proporção, a soma dos antecedentes está para a soma dos consequentes, assim como qualquer antecedente está para o consequente.  Esquematicamente:
a/b = c/d ---> (a+c)/b+d = a/b ou (a+c)/b+d = c/d 

5. Em toda proporção, a diferença dos antecedentes está para a diferença dos consequentes, assim como qualquer antecedente está para o consequente, ou seja:
a/b = c/d ---> (a-c)/b-d = a/b ou (a-c)/b-d = c/d 

6. Em toda proporção, o produto dos antecedentes está para o produto dos consequentes, assim como o quadrado de um antecedente está para o quadrado de seu consequente, ou seja:

7. Em toda proporção, elevando-se os quatro termos ao quadrado, resulta uma nova proporção, ou seja:

Exercícios Resolvidos







1. Se a soma de dois números vale 80 e a razão entre o menor e o maior é 2/3.  Quais são os números?
a+b=80
a/b = 2/3  ---> (a+b)/b=(2+3)/3 --->(a+b)/b=5/3 --->80/b=5/3
--->80.3=b.5 --->240=5b --->b=240/5 --->b=48
como: a+b=80 ---> a=80-b --->a=80-48 ---> a=32
provando: a/b=2/3 --->32/48=2/3 (divide-se 32/16=2 e 48/16=3)

2. Determine dois números sabendo-se que a razão entre eles vale 7/3 e a diferença entre eles vale 48.
a/b=7/3
a-b=48 --->(a-b)/b=(7-3)/3 --->48/b=4/3 --->48.3=4b --->144=4b
b=144/4 --->b=36  
como a-b=48 --->a=48+b--->a=48+36 --->a=84
Logo os números são: 84 e 36

3. A área de um retângulo é 150 m2 e a razão da largura para o comprimento é 2/3. Quais são as medidas da figura?
a=largura   b=comprimento

Exercícios com resposta - Se tiverem dúvidas na solução  de algum dos exercícios, deixem um comentário que posto a solução.

1. A soma dos quadrados de dois números vale 468 e a razão do maior para o maior é 2/3. Quais são esses números? Resposta: 12 e 18

2. A soma dos quadrados de dois números vale 452 e a razão do maior para o maior é 7/8. Quais são esses números? Resposta: 14 e 16

3. Calcule a e b, sabendo-se que a+b=63 e que a/3=b/4. Resp. a=27 e b=36

4. Calcule a e b, sabendo-se que a-b=26 e que a/7=b/5. Resp. a=91e b=65

5. A área de um retângulo vale 200 m2 e a razão da largura para o seu comprimento vale 1/2.  Quais são as medidas do retângulo?
Resposta: largura= 10 e comprimento= 20

Bons Estudos