Equação do Segundo Grau
É uma equação composta por uma incógnita representada por uma variável (x, y, z, ...), cujo grau maior da incógnita ou variável é dois e possui três coeficientes reais (a, b e c), sendo que o coeficiente "a" necessariamente deve ser um número diferente de zero .
Também chamamos uma Equação do Segundo Grau de Equação Quadrática.
É representada por: ax² + bx + c = 0, de variável x e {a,b,c} Є Reais, com a≠0.
Gráfico da parábola.
Ela representa uma parábola.
As raízes ou zeros da equação são os pontos: (x1, 0) e (x2, 0) que pertencem ao eixo Ox do sistema cartesiano.
Ela também corta o eixo Oy no ponto (0,c) do sistema cartesiano.
Concavidade da parábola.
Sabemos que ela pode ter a concavidade voltada para cima ou para baixo, dependendo do sinal do coeficiente "a":
- Quando o valor do coeficiente "a" for negativo, a concavidade será para baixo,
- Quando o valor do coeficiente "a" for positivo, teremos concavidade pra cima.
Exemplo 1
Gráfico da equação: x²-5x+6=0, que tem raízes: x1=2 e x2=3, c=6
Observe que a=1 ou a>0
Exemplo 2
Gráfico da equação: -x²-x+2=0, que tem raízes: x1=1 e x2=-2, c=2
Observe que a=-1 ou a<0
Coeficientes da parábola.
Veja nos exemplos, o valor dos coeficientes das equações quadráticas abaixo:
a) 2x²+3x+2=0,
a=2, b=3 e c=2
b)-3x²-4x-3=0
a=-3, b=-4 e c=-3
c) x²+13x+12=0
a=1, b=13 e c=12
Nota: Quando a equação possuir todos os termos ela é chamada de equação completa do segundo grau.
Caso contrário ela será uma equação incompleta, porém é necessário sempre que o coeficiente "a"que esta associado ao x² seja diferente de zero.
Caso contrário ela será uma equação incompleta, porém é necessário sempre que o coeficiente "a"que esta associado ao x² seja diferente de zero.
Exemplos:
c) 3x²=0
a=3, b=c=0
d) -4x²+3x=0
a=-4, b=3, c=0
Resolução da Equação Quadrática
História da Equação do Segundo Grau.
Inicialmente, ela foi estudada pelo matemático Sridhara, que obteve a Fórmula, mas ficou conhecida como Fórmula de Bhaskara, pois foi Bhaskara que a publicou na época. É utilizada para solucionar as equações do segundo grau, ou seja descobrir as raízes que satisfaçam a equação. Um fato curioso é que a Fórmula de Bhaskara não foi descoberta por ele, mas pelo matemático hindu Sridhara, pelo menos um século antes da publicação de Bhaskara, acontecimento reconhecido pelo próprio Bhaskara, embora o material construído pelo pioneiro não tenha chegado até nós.
O fundamento usado para obter esta fórmula foi buscar uma forma de reduzir a equação do segundo grau a uma do primeiro grau, através da extração de raízes quadradas de ambos os membros da mesma.
Para resolver uma equação do segundo grau, temos que substituir na fórmula abaixo os valores dos coeficientes a, b e c e efetuar os cálculos para achar os valores de x (ou outra variável) que satisfaçam a equação.
Observação: ∆ é chamado de discriminante da equação e vale b²-4ac
Agora veja a fórmula de Bhaskara:
Agora veja a fórmula de Bhaskara:
Por exemplo:
Resolva a equação: -x²+2x+8=0
i) Achemos o valor do ∆ = b²-4.a.c, onde a=-1, b=2 e c=8
∆ = b²-4ac
∆ = 2²-4.(-1).8
∆ = 4+32
∆ = 36
ii)Substituindo a,b,c e ∆ na equação:
-x²+2x+8=0
Prova: Se colocarmos na equação, o valor de x=-2 ou x=4, a mesma terá de se anular nestes dois pontos, motivo pelo qual as raízes também são chamadas de zeros da equação.
para x=-2, temos:
-x²+2x+8=0 ---> -(-2)²+2.(-2)+8 =
=-4-4+8
=-8+8
=0
para x=4, temos:
-x²+2x+8=0 ---> -(4)²+2.(4)+8 =
=-16+8+8
=-16+16
=0
Discriminante da equação do 2° grau
Achar o valor do discriminante é muito importante, pois através deste valor podemos determinar o número de raízes de uma equação do segundo grau.
Como visto acima, o discriminante é representado pela letra grega Δ e equivale à expressão b2 - 4ac, isto é: Δ = b2 - 4ac.
1) Quando Δ < 0
Caso Δ < 0, a equação não tem raízes reais, pois 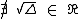 :
:
2) Quando Δ = 0
Caso Δ = 0, a equação tem duas raízes reais e iguais, ou seja: 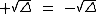 :
:
3) Quando Δ > 0
Caso Δ > 0, a equação tem duas raízes reais e são diferentes, pois 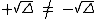 :
:
A - Determine o valor dos coeficientes das equações quadráticas abaixo:
1) 2 x² + 7x + 5 = 0,
2) 3 x² + x + 2 = 0,
3) x² -7 x + 10 = 0,
4) 5x² - x -3 = 0,
Veja a resposta na postagem com data posterior.
B - Calcular o discriminante de cada equação:
a) x² + 9 x + 8 = 0 (R:49)
b) 9 x² - 24 x + 16 = 0 (R:0)
c) x² - 2 x + 4 = 0 (-12)
d) 3 x² - 15 x + 12 = 0 (R: 81)
e) 5x² - 3x - 2 = 0 (R: 49)
f) x² - 10x + 25 = 0 (R: 0)
g) x² - x - 20 = 0 (R: 81)
h) x² - 3x -4 = 0 (R: 25)
i) x² - 8x + 7 = 0 (R: 36)
C - RESOLVA AS EQUAÇÕES DE 2º GRAU
1) x² - 5x + 6 = 0 _____(R:2,3)
2) x² - 8x + 12 = 0 ______(R:2,6)
3) x² + 2x - 8 = 0______ (R:2,-4)
4) x² - 5x + 8 = 0 ______(R:vazio)
5) 2x² - 8x + 8 = 0_______ (R:2)
6) x² - 4x - 5 = 0_______ (R:-1, 5)
7) -x² + x + 12 = 0_______ (R:-3, 4)
8) -x² + 6x - 5 = 0_______ (R:1,5)
9) 6x² + x - 1 = 0______ (R:1/3 , -1/2)
10) 3x² - 7x + 2 = 0 ______(R:2, 1/3)
11) 2x² - 7x = 15 _______(R:5, -3/2)
12) 4x² + 9 = 12x______ (R:3/2)
13) x² = x + 12 ______(R:-3 , 4)
14) 2x² = -12x - 18 _____(R:-3 )
15) x² + 9 = 4x_____ (R: vazio)
16) 25x² = 20x – 4 ____(R: 2/5)
17) 2x = 15 – x² ______(R: 3 , -5)
18) x² + 3x – 6 = -8____ (R:-1 , -2)
19) x² + x – 7 = 5 ____(R: -4 , 3)
20) 4x² - x + 1 = x + 3x² ___(R: 1)
21) 3x² + 5x = -x – 9 + 2x²____ (R: -3)
22) 4 + x ( x - 4) = x _____(R: 1,4)
23) x ( x + 3) – 40 = 0 _____(R: 5, -8)
24) x² + 5x + 6 = 0 _____(R:-2,-3)
25) x² - 7x + 12 = 0 _____(R:3,4)
26) x² + 5x + 4 = 0 _____(R:-1,-4)
27) 7x² + x + 2 = 0 _____(vazio)
28) x² - 18x + 45 = 0 _____(R:3,15)
29) -x² - x + 30 = 0 _____(R:-6,5)
30) x² - 6x + 9 = 0 _____(R:3)
31) ( x + 3)² = 1_______(R:-2,-4)
32) ( x - 5)² = 1_______(R:6,4)
33)( 2x - 4)² = 0_______(R:2)
34) ( x - 3)² = -2x²_______(R:vazio)
Qualquer dúvida deixe um comentário na postagem.
Bons Estudos!
----------------------------------------------------------------------------------------------------------------------------------
Resposta dos exercícios da postagem anterior (Regras de Sociedade)
1. A, B e C constituíram uma sociedade mercantil, entrando cada um respetivamente com: 7.000,00, 8.500,00 e 9.000,00 de capitais. O sócio A ficou 1 ano, B ficou 8 meses e C apenas 7 meses na empresa. Neste período apurou-se um prejuízo de 21.500,00 que deveria ser ressarcido proporcionalmente por eles. Quanto em moeda, cada um deve desembolsar?
Prejuízos: A = 8.400,00, B=6.800,00 e C= 6.300,00
2. Três pessoas: Henrique, José e Katia, formam uma sociedade em que cada uma delas entrou respectivamente com os seguintes capitais: 14 mil, 17 mil e 18 mil reais. Henrique ficou na empresa por um ano, José ficou 8 meses e Katia ficou apenas 7 meses. A empresa obteve um lucro líquido de R$ 64.500,00. Como deveremos apurar os valores de cada um?
Lucros: Henrique = 25.200,00, José = 20.400,00, Kátia = 18.900,00
3. A, B e C são pessoas que fundaram uma loja, sendo que A alocou 100 mil e ficou na sociedade por dois anos, B alocou 50 mil e permaneceu por 3 anos na empresa, enquanto que C entrou com 150 mil e ficou um ano e meio trabalhando na empresa como sócio. Após o período de 3 anos a loja foi extinta e sendo apurado um lucro nesse período. Sabe-se que B recebeu 20 mil reais a menos que A. Quanto recebeu cada sócio?
Lucro dos sócios: A= 80.000,00, B= 60.000,00 e C= 90.000,00
4. Se a diferença entre os valores recebidos (lucro) pelos dois sócios mais velhos da Empresa X foi de R$ 10.000,00 e a firma tem 4 sócios e todos aplicaram capital iguais de 100 mil reais, sendo que o sócio A permaneceu 5 anos, B ficou 10 anos, C, 20 anos e D, 25 anos. Quanto recebeu cada um ao final do período?
Lucros recebidos por: A = 2.000,00, B= 20.000,00, C= 40.000,00 e D= 50.000,00
----------------------------------------------------------------------------------------------------------------------------------









Realmente este conteúdo foi em pouco tempo muito bem detalhado.
ResponderExcluirObrigado, continue estudando este assunto.
ExcluirQualquer dúvida, estamos a disposição.