Noções de Estatistica

INTRODUÇÃO A ESTATÍSTICA

HISTÓRICO

Todos os dias, ouvimos pela TV ou lemos nos jornais, sobre as atividades relacionadas com algumas pesquisas realizadas nos mais diversos campos ou áreas científicas, como saúde, educação, sociologia, trabalho, loterias, etc.. Se você abrir um jornal, uma revista ou qualquer outra mídia, verá uma infinidade de dados expostos em gráficos, pesquisas, lançamentos de novos produtos, etc.  Tudo isso, demanda muitos trabalhos estatísticos, porque ninguém em sã consciência colocará recursos em algo que não trará bons retornos.

Esses estudos levam em consideração, determinados aspectos que relacionam etapas do trabalho, com o intuito de facilitar a comunicação e ainda, apresentar os resultados de forma mais coerente.

O uso da pesquisa é bastante comuns nas mais diversas atividades humanas. Por exemplo:

·       Antes do lançamento de um novo produto no mercado, as indústrias costumam realizar pesquisas entre os consumidores, para saber sobre a aceitação desse produto, antes do lançamento;

·        Nas campanhas eleitorais, os candidatos costumam realizar pesquisas, no sentido de obter subsídios ou elementos para o direcionamento da campanha;

·        Para organizar sua programação, as emissoras de TV utilizam das pesquisas para direcionar ou organizar sua programação;

·       Os sócios quando pretendem abrir um negócio necessitam de um plano de negócio que apresentará muitas pesquisas e previsões de retorno de capital, etc.

Essas pesquisas envolvem muitas etapas, tais como, a escolha da amostra, a coleta e organização dos dados (tratamento da informação), resumo dos dados (em tabelas, gráficos, etc.) e a interpretação dos resultados.

A parte da matemática que trata desses assuntos é a Estatística.

CONCEITO DE ESTATÍSTICA

 A Estatística é a parte da Matemática que trata dos métodos científicos para coleta, organização, resumo, apresentação e análise dos dados.

De origem muito antiga, a Estatística teve durante séculos um caráter meramente descritivo e de registro de ocorrências. As primeiras atividades datam 2000 a.C. e referem-se a iniciativas de realizar cadastramento ou recenseamento das populações agrícolas chinesas.

O que modernamente se conhece como Estatística, é um conjunto de técnicas e métodos de pesquisa que, entre outros tópicos, envolve o planejamento do experimento a ser realizado, a coleta qualificada dos dados,  a inferência e o processamento e análise das informações.

ETAPAS DO TRABALHO ESTATÍSTICO.

Em um trabalho estatístico podemos admitir as seguintes etapas:

A) COLETA DE DADOS, a partir de uma amostra escolhida da população.

Essa é a etapa inicial do trabalho estatístico e consiste, principalmente, em recolher os dados brutos, realizados a partir da amostra escolhida no universo estatístico;

B) ANÁLISE DESCRITIVA, com resumo e interpretação dos dados coletados.
É a fase do trabalho estatístico, que descreve através de um resumo, a interpretação dos dados coletados;

C) MODELO EXPLICATIVO,  É a fase do trabalho estatístico que procura explicar o comportamento do objeto em estudo, a fim de fazer, numa
etapa posterior, a análise confirmativa dos dados, também conhecida como inferência.

TRATAMENTO DAS INFORMAÇÕES.

Para o tratamento dessas informações, a Estatística pode ser dividida em: descritiva e indutiva.

A Estatística descritiva descreve e analisa um conjunto de dados, sem tirar conclusões.

A Estatística indutiva ou Inferência estatística trata das inferências e conclusões, ou seja, com base na análise de dados são tiradas as conclusões.

A parte da Estatística que nos interessa é a da Estatística Descritiva, pois é ela que organiza, descreve e analisa os dados experimentais colhidos, apresentando-os em tabelas e gráficos de modo a tornar mais compreensivas e interessantes as pesquisas.

Para iniciar o nosso estudo sobre a Estatística, vamos definir alguns conceitos preliminares e importantes que fazem parte do tratamento da informação e nos ajudam a compreender e avaliar essas informações que chegam a toda hora pelos mais diversos meios de comunicação.

Imagine a seguinte situação:

Durante um telejornal, o repórter divulgou uma pesquisa segundo a qual apenas 5% dos brasileiros têm o hábito de ler jornal diariamente.

Você já pensou como são feitas as pesquisas como essa? Como é possível entrevistar toda a população brasileira para se saber a porcentagem de leitores de jornal?

Veremos que no estudo da estatística, não é necessário entrevistar toda a população para se chegar a uma determinada conclusão sobre ela.

Chegar a esse tipo de conclusão também é o objeto da Estatística.

NOÇÃO DE POPULAÇÃO OU UNIVERSO ESTATÍSTICO.

A Estatística parte da observação de grupos, geralmente numerosos, aos quais damos o nome de população ou universo estatístico.

A cada elemento da população estudada, denominamos de unidade estatística ou elemento.

Assim, quando é feita uma coleta de dados sobre um determinado assunto, chama-se universo estatístico ou população estatística o conjunto formado por todos os elementos que possam oferecer dados pertinentes ao assunto em questão.

Dessa forma Universo Estatístico ou População Estatística é o conjunto de todos os elementos que compõem o estudo em questão.

Exemplos de População

a) O governo brasileiro encomenda ao IBGE (Instituto Brasileiro de Geografia e Estatística), uma pesquisa para conhecer o salário médio do brasileiro.
O universo estatístico ou a população estatística é nesse caso, o conjunto de todos os assalariados brasileiros.

b) Um partido político quer conhecer a tendência do eleitorado quanto à preferência entre dois candidatos à Presidência do Brasil. 

Para isso, encomenda uma pesquisa a uma empresa especializada. O universo estatístico ou população estatística é, nesse caso, o conjunto de todos os eleitores brasileiros.

AMOSTRA.

Quando o universo estatístico é muito grande ou quando não é possível coletar dados de todos os seus elementos, retira-se desse universo um subconjunto, chamado de amostra, no qual os dados são coletados.

Dessa forma, a amostra considera apenas uma pequena parte do todo (do universo).
Cada elemento que compõe a amostra é um indivíduo ou objeto.

Exemplos:

a) Numa pesquisa sobre as eleições, a população é formada por todos os cidadãos com direito a voto e a amostra é formada pelos eleitores que serão entrevistados e os indivíduos são as pessoas que serão entrevistadas.

b) Numa pesquisa para se verificar a durabilidade das marcas de lâmpadas dos diversos fabricantes, cada marca é um objeto da pesquisa.


VARIÁVEL.

Em Estatística, uma variável é um atributo mensurável que varia tipicamente entre os indivíduos.

Dessa forma, a observação da população é dirigida ao estudo de uma dada propriedade ou característica dos elementos dessa população ou desse universo estatístico.

Exemplos:

A cor de um veículo, o sexo de uma criança, a idade de um jovem, etc., são variáveis das pesquisas.

Quanto ao tipo, as variáveis podem ser:

1. Qualitativa – São aquelas que apresentam uma qualidade ou um atributo sobre o “indivíduo” pesquisado.  Se baseiam em qualidades e não podem ser mensuráveis. São atributos que não apresentam números em sua constituição, tais como: raça, área de estudos, meio de transporte, etc.

Podem ser subdivididas em:

a) Variável qualitativa ordinal – Quando podem ser colocadas em ordem. Exemplo: a classe social (A, B, C, D ou E).

b) Variável qualitativa nominal – Quando não podem ser hierarquizadas ou ordenadas. Exemplo: cor dos olhos, local de nascimento.

2. Quantitativa – Aquelas que se apresentam em formas de valores ou números, tais como: altura, peso, idade em anos, número de irmãos, etc.

Quando uma variável pode assumir qualquer valor real entre dois valores dados é chamada de variável contínua.

Caso isso não seja possível, a variável é chamada de variável discreta.

Por isso as variáveis quantitativas, podem ser subdivididas em:

a) Variável Quantitativa Discreta. Quando não pode assumir todos os valores das variáveis, ou seja, assumem valores dentro de um espaço finito ou enumerável, tipicamente números inteiros. Um exemplo é o número de filhos de uma pessoa;

b) Variável Quantitativa Contínua. Quando pode assumir todos os valores de um conjunto contínuo, tipicamente os números reais. Por exemplo: o peso ou a altura de uma pessoa.

Conclusão: Dessa forma, as contagens resultam em variáveis discretas e as medições resultam em variáveis contínuas;


Por exemplo:

Os resultados do lançamento de um dado podem assumir os valores 1, 2, 3, 4, 5 ou 6, mas não os valores intermediários iguais a 2,3 ou 3,2; portanto, a variável é uma variável discreta.

Já os pesos ou as alturas de um conjunto de pessoas podem assumir, teoricamente, qualquer valor; portanto, é uma variável contínua.

FREQUÊNCIA.

Já vimos que os valores distribuídos ou assinalados de forma aleatória numa amostragem são denominados DADOS BRUTOS. Ao número de vezes que uma variável se apresenta, ou se repete numa amostragem, denominamos de freqüência.

DISTRIBUIÇÃO DE FREQUÊNCIA.

Uma DISTRIBUIÇÃO DE FREQUÊNCIA ocorre quando os valores são indicados ou agrupados de uma forma ordenada levando-se em consideração os seus extremos.

O primeiro passo para obtenção de informações mais resumidas e precisas a respeito do comportamento das variáveis, é a construção das tabelas de freqüência.

Uma tabela de freqüência é encontrada quando para cada variável estudada, contamos o número de vezes que a variável aparece, em realizações ou valores.

Essa nova tabela encontrada é denominada TABELA DE FREQUÊNCIA.

Uma tabela de freqüência pode se apresentar de forma absoluta (FA) ou forma relativa (FR).

Considerando o exemplo sobre os freqüentadores do cinema, para a variável Estado Civil, encontramos os seguintes valores absolutos:

Solteiro: 9 casado: 8 separado: 3

Observe-se que a freqüência absoluta não é uma medida muito significativa para a análise de dados, especialmente se desejamos comparar a distribuição da mesma variável em populações (universo) diferentes.

Assim, precisamos definir uma medida que considere o total das observações colhidas.

Essa medida é a freqüência relativa.

A freqüência relativa é definida como a razão entre a freqüência absoluta e o total de observações:

FR (Freqüência relativa) = Frequência absoluta / total de observação

Exemplo:

Numa favela com mais de 50 mil moradores, foi feita uma pesquisa com um grupo de 20 pessoas sobre qual dos problemas: habitação, educação, segurança ou saúde era para eles o mais crítico.  A lista abaixo é o resultado desta pesquisa:

Habitação                         Saúde                          Educação                              Educação

Segurança                         Habitação                    Saúde                                   Segurança

Habitação                         Segurança                    Segurança                             Saúde

Segurança                         Segurança                    Habitação                             Saúde

Segurança                         Segurança                    Segurança                             Segurança

Contamos o número de pessoas que apontaram a habitação temos: 4; saúde 4; segurança 10 e educação 2.  Neste caso são essas as frequências absolutas(FA).

A taxa percentual representa as Frequências relativas (FR) que é obtida dividindo-se a FA pelo total e multiplicando-se por 100.

Veja:

FR (%) da habitação: (4/20).100 = 20% , etc...

Problema	Frequência(FA)	Taxa Percentual(FR)
Habitação	4	20%
Segurança	10	50%
Saúde	4	20%
Educação	2	10%
Totais	20	100%

Vamos agora passar esses dados num gráfico de setores que consiste em dividir em setores de áreas proporcionais às taxas percentuais, poderemos apreciar melhor a referida pesquisa.

Como a circunferência tem 360º, vamos dividi-la  proporcionalmente as porcentagens acima: 

Veja tabela abaixo 

Habitação 20% de 360º =0,20x360º =72º

Segurança 50% de 360º =0,50x360º =180º

Saúde 20% de 360º =0,20x360º =72º

Educação 10%de 360º =0,10x360º =36º

Com ajuda do compassso e do transferidor, passamos os dados  para o gráfico de setores:

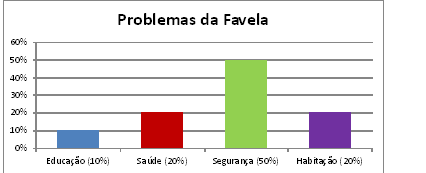
Se quisermos inserir os dados num gráfico de barras verticais, então colocaríamos:
- No eixo vertical - as frequências absolutas (FAs) e no horizontal o nome dos respectivos                 problemas que são as variáveis qualitativas no caso acima.

Ou, ainda podemos colocar os dados da seguinte maneira: No eixo vertical as frequências relativas (FRs) e no eixo horizontal o nome das variáveis pesquisadas.  Veja gráfico abaixo:

--------------------------------------------------------------------------------------------------------------------------

Exercício para fixação - Se tiver alguma dúvida, deixe seu comentário logo abaixo que esclarecemos o mais breve possível!

Numa das delegacias de uma grande cidade há uma tabela de pessoas que se queixaram de roubo ou furto de carteira.  Na última semana, a referida tabela apresentava os seguintes dados:

Dia da Semana	Nº de queixas
Segunda	10
Terça	10
Quarta	15
Quinta	20
sexta	35
Sábado	5
Domingo	5
Total	100

Faça:

a) a tabela com a distribuição da frequência absoluta e a taxa percentual;

b) o gráfico de setores.

Nota: Se você quer saber todo conteúdo sobre: Média, Mediana, Moda com muitos exercícios que foram cobrados em exames do ENEM, acesse o post: Média, Mediana e Moda -Resolução de Questões do ENEM.

-------------------------------------------------------------------------------------------------------------------------
Bons Estudos