Semelhança em Triângulos
No estudo da Geometria Plana, dizemos que dois triângulos são semelhantes, quando apresentam uma determinada proporção entre eles, ou seja quando os ângulos e os lados do primeiro triângulo, estão em correspondência com os ângulos e lados de um segundo triângulo, de tal forma que seus ângulos têm as mesmas medidas e os lados do primeiro triângulo forem proporcionais aos lados do segundo.
Os critérios de proporcionalidade que vamos discutir agora e que figuram na semelhança de triângulos, são aplicados em muitas outras figuras como: polígonos, entre outras.
Revisando, aprendemos que triângulos são polígonos que possuem três lados, três ângulos internos cuja soma vale 180º e que se classificam em: Equiláteros (3 lados iguais), Escaleno (3 lados diferentes) e Isósceles ( 2 lados iguais).
Ainda, se ele tiver um dos ângulos medindo 90º (reto) é chamado de Triângulo Retângulo.
Esclarecemos também que o estudo que é feito para identificar a semelhança de figuras poligonais será válido também para o estudo da semelhança de triângulos.
Dois triângulos serão semelhantes, se satisfizerem duas condições simultaneamente:
1) Se seus lados correspondentes possuírem medidas proporcionais e;
2) Se os ângulos correspondentes forem iguais (ou congruentes).
Uma vez aplicadas as afirmações feitas acima, teremos um fato verdadeiro, ou seja, as condições estarão satisfeitas somente quando os triângulos são semelhantes.
Vejamos um desenho ilustrativo, para que possamos compreender melhor o critério ora abordado:
Uma vez aplicadas as afirmações feitas acima, teremos um fato verdadeiro, ou seja, as condições estarão satisfeitas somente quando os triângulos são semelhantes.
Vejamos um desenho ilustrativo, para que possamos compreender melhor o critério ora abordado:
Antes, temos que determinar a correspondência dos vértices de cada triângulo, pois assim determinaremos a correspondência dos lados e dos ângulos entre estes dois triângulos.
Os vértices A, B, C correspondem, respectivamente, aos vértices A’, B’, C’. Sendo assim, montaremos as razões de proporcionalidade entre os lados correspondentes.

Uma das condições é que todos os lados correspondentes possuam uma proporcionalidade, que chamaremos neste caso de k. Ressaltando que essa razão foi construída pela divisão de cada lado correspondente: veja que o lado A’B’ do segundo triângulo corresponde ao lado AB do primeiro triângulo. Por este fato, a divisão foi feita entre eles, e de mesmo modo com os outros lados.
Entretanto, apenas a condição de proporcionalidade dos lados não é suficiente para afirmarmos a semelhança entre os dois triângulos. Necessitamos que seus ângulos correspondentes sejam iguais.
Sendo assim, indicaremos a semelhança destes triângulos desta forma:
Exemplo:
Verifique se os triângulos a seguir são proporcionais.
Verificarmos a congruência dos ângulos, no destaque acima.
Temos agora que verificar a proporcionalidade dos lados.
Temos agora que verificar a proporcionalidade dos lados.
Note que todos os lados possuem a mesma razão de proporcionalidade (1/2).
Sendo assim, podemos afirmar que
Exercícios:
1) Determine x e y nos seguintes pares de triângulos semelhantes:
a)
∆ABC ~ ∆A’B’C’ à AB/A’B’ = AC/A’C’ = BC/B’C’
6/2 = 12/y = x/3
6/2 = 12/y à 6y = 2.12 à 6y = 24 à y= 24/6 à y=4 cm
6/2 = x/3 à 2x = 6.3 à 2x = 18 à x= 18/2 à x= 9 cm
.................................................................................................................................................................................
b)
∆ABC ~ ∆AED à AB/AE = AC/AD = BC/ED
9/6 = 12/X à 9X = 6.12 à 9X = 72 à X = 72/9 à X= 8 CM
9/6 = Y/4 à 6Y = 9.4 à 6Y = 36 à Y= 36/6 à Y= 6 CM
2) Determine x e y nos seguintes pares de triângulos semelhantes:
Solução:
a) (12+y)/y =( x+5)/5 = 12/3
i) de (12+y)/y = 12/3 à (12+y)3 = 12y à 36+3y = 12y à 36 = 12y-3y à 36 = 9y à
y=36/9 à y= 4
ii) de (x+5)/5 = 12/3 à (x+5)3 = 5.12 à 3x+15 = 60 à 3x= 60-15 à 3x= 45 àx= 45/15 à x= 15
................................................................................................................................................................................
b) 12/9 =(y+12)/12 = (x+5)/x
i) 12/9 = (y+12)/12 à 12.12 = 9(y+12) à 144 = 9y+108 à 144-108= 9y à 36 = 9y à y= 36/9 à y= 4
ii) 12/9 = (x+5)/x à 12x = 9(x+5) à 12x = 9x+45 à 12x-9x = 45 à 3x = 45 à x= 45/3 à x= 15
.................................................................................................................................................................................
Atenção:
a) Caso você queira estudar gratuitamente o teorema de tales, que abrange tema importantíssimo da geometria, inclusive com muitos exercícios, acesse o post chamado Teorema de Tales, ou se preferir, clique aqui!
b) Se ficou alguma dúvida, ou ainda quiser comentar, para acrescentar, retificar, elogiar ou mesmo criticar, utilize o espaço abaixo para comentários. Desde já, agradecemos seu parecer e também a sua visita!
 |
| A Matemática Aqui é Simples e Descomplicada! |




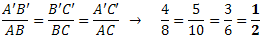






Obrigado, seu blog vai me ajudar demais em Matemática na minha escola...
ResponderExcluirCaro leitor, esse é o nosso objetivo, continue sempre nos prestigiando.
Excluir