Matrizes

Curiosidades Sobre as Matrizes e a Matemática

As matrizes tiveram sua importância acentuada e se distanciaram dos estudos dos determinantes, somente há quase 150 anos.  O seu descobrimento pode ter sido creditdo ao matemático Cauchy, 1826, e ela inicialmente e até hoje foi nomeada como: tableau ou tabela.  O nome atribuido como matriz só foi utilizado depois por James Joseph Sylvester, 1850. Mas, foi o matemático Cayley, quando publicou a famosa obra: Memoir on the Theory of Matrices, 1858, que divulgou o assunto e começou a demonstrar a sua utilidade nas ciências.
Mesmo que não queiramos, mas quando utilizamos tabelas em joguinhos infantis,  em brincadeiras diversas ou mesmo em nosso computador (software de planilhas excel), estamos utilizando tabelas ou matrizes, daí a importância que ela ainda exerce em muitas atividades em nosso dia a dia. 

As matrizes são muito ulizadas na engenharia elétrica e também em outras áreas do conhecimento como a computação, matemática e estatística.  Ela é muito utilizada em programas de computadores e/ou calculadoras programáveis específicas para resolver sistemas muito complexos e de uma maneira simples e rápida. 

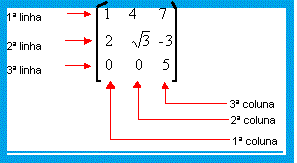
Considerações Iniciais
Observe os seguintes conjuntos numéricos, onde os elementos estão dispostos em linhas e colunas e colocados entre parênteses ou barras duplas:

Matriz Quadrada - É aquela em que o número de linhas é igual ao número de colunas.
Matriz Linha - É aquela que possui apenas uma linha.
Matriz Coluna - É aquela que possui apenas uma coluna.

Exemplos:
1) A= |2|  →é uma matriz quadrada de ordem 1.
2) C= |1  2  3  4  5| →é uma matriz LINHA de ordem 1x5.
3) Matriz Quadrada de ordem 3

|1	2	3|
|4	5	6|
|7	8	9|

4) Matriz Coluna de Ordem 4x1 

1

2

2

4

Notação Genérica:

Representamos genericamente uma matriz do tipo m x n escolhendo uma letra minúscula do nosso alfabeto com dois índices para representar cada um dos seus elementos, de modo que o primeiro índice à esquerda, indique a que linha o elemento pertence, enquanto que o segundo índice da direita indique a coluna que o elemento pertence.
Veja o esquema abaixo da matriz A:

Observações: 1) O elemento a1,3 pertence a 1ª linha e 3ª coluna;
                      2) O elemento a2,3 pertence a 2ª linha e a 3ª coluna.
                      3) A matriz acima tem m linhas e n colunas.
Notação Abreviada: Também podemos representar essa matriz A tomando-se um elemento genérico aij, onde 1=<i<=m e 1=<j<=n, ou A=(aij)mxn.

Exemplo: Construa uma matriz A=(aij) do tipo 2 x 3, sendo que: aij=i+j.
Sabemos que ela será do tipo: 

Então, calculemos seus elementos aplicando-se a regra que pede: aij=i+j:
a11 = 1+1 =2
a12 = 1+2 =3
a13 = 1+3 =4
a21= 2+1 =3
a22 = 2+2=4
a23 = 2+3=5

Então, abaixo temos a matriz A: 

Exercícios:

1.Usando a matriz A acima, quais são os elementos: a(23), a(13)e a(34)?
a23=5 
a13=4
a34=Não existe

2.Construa uma matriz B= (bij) do tipo 2 x 3, sendo bij = 2i+j.
B=| b11  b12  b13|
     | b21  b22  b23| 
Calculemos os seus elementos usando a regra bij=2i+j:
b11 =2.1+1 =2+1=3
b12 =2.1+2 =2+2=4
b13 = 2.1+3=2+3=5
b21= 2.2+1=4+1=5
b22= 2.2+2=4+2=6
b23 =2.2+3=4=3=7

Então: B =  |3  4  5|  

                   |5  6  7|