A Ideia de Número Fracionário
A ideia de número fracionário
Veja a figura ao lado, o que será que as divisões têm em comum?
Adiantamos que tratam-se da mesma fração 1/2 ou meio, ou sejam representam a mesma parte do todo e elas são chamadas frações equivalentes.
Mas, de um modo geral, todos os números naturais também representam frações. Vejamos:
1) Para exprimirmos o número de elementos de um conjunto finito empregamos um só número natural.
2) Para expressarmos, matematicamente, uma parte ou algumas partes de um todo, vamos usar um par ordenado de números naturais.
Nota: Os pares de números naturais: 1/2 e 2/5 são chamados frações ou números fracionários.
Então: Chamamos de fração a todo par ordenado de números naturais, com o segundo diferente de zero, onde:
a) o primeiro número indica quantas partes tomamos do inteiro.
b) o segundo número indica em quantas partes iguais o inteiro foi dividido.
Exercícios:
1) Observando os exemplos abaixo, expresse qual fração da figura toda é a parte colorida, supondo que sejam divididas em partes iguais:
Solução: a) 1/4, b) 2/3 e c) 5/6
2) Agora você deverá colorir a parte indicada pelas frações abaixo:
.jpg)
2 3 4
5 6 7 8 9
10 11 12 13 14 15 16
- - - - - - - - -
- - - - - - - - - - -
3. O algarismo das unidades do número N= 1x3x5x7x9x ... x999 é igual a:
Resposta: Observe que todos os números do produto, são ímpares, e além disso o produto de qualquer número ímpar por 5 termina com o algarismo 5. Logo, a opção correta é o 5.
4. Qual é a metade do dobro do dobro da metade de 2?
Filho é igual a A
Pai é igual a B
Mãe é igual a C
Avô é igual a D
Tio é igual a E
Pergunta-se: Qual é o A do B da C do A?
Resposta: Qual é o filho do pai da mãe do filho?
Resposta: É o tio que é igual a E.
...........................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Para voltar para a postagem anterior, clique no botão voltar à esquerda ou acesse: Teste de Raciocínio Matemático, ou clique aqui!
Veja a figura ao lado, o que será que as divisões têm em comum?
Adiantamos que tratam-se da mesma fração 1/2 ou meio, ou sejam representam a mesma parte do todo e elas são chamadas frações equivalentes.
Mas, de um modo geral, todos os números naturais também representam frações. Vejamos:
1) Para exprimirmos o número de elementos de um conjunto finito empregamos um só número natural.
2) Para expressarmos, matematicamente, uma parte ou algumas partes de um todo, vamos usar um par ordenado de números naturais.
Nota: Os pares de números naturais: 1/2 e 2/5 são chamados frações ou números fracionários.
Então: Chamamos de fração a todo par ordenado de números naturais, com o segundo diferente de zero, onde:
a) o primeiro número indica quantas partes tomamos do inteiro.
b) o segundo número indica em quantas partes iguais o inteiro foi dividido.
Exercícios:
1) Observando os exemplos abaixo, expresse qual fração da figura toda é a parte colorida, supondo que sejam divididas em partes iguais:
Solução: a) 1/4, b) 2/3 e c) 5/6
2) Agora você deverá colorir a parte indicada pelas frações abaixo:
Solução:
Observações importantes:
1. Numa fração, o primeiro número chama-se numerador enquanto que o segundo número chamamos de denominador e ambos constituem os termos de uma fração.
Exemplo: Na fração 1/2 temos que 1 é o numerador e 2 é o denominador.
Na fração 3/5, 3 é o numerador e 5 é o denominador.
2. Ficou claro pelo que já vimos, que não existem frações com denominador zero. Exemplo: As frações a seguir não existem: 2/0, 3/0, etc.
3. Fração própria é aquela, cujo numerador é menor que o denominador. Ex. 2/3, 1/2, 5/7, ...
4. Fração imprópria é aquela, cujo numerador é maior que o denominador. Ex. 5/4, 3/2, 10/9, ...
5. Frações aparentes são aquelas, cujo numerador é múltiplo do denominador e são consideradas como números naturais. Ex. 3/3 vale 1, 8/4 vale 2, 16/2 vale 8, 9/3 vale 3, ...
6. Quando o denominador vale 10 ou é uma potência de 10, a fração é chamada de fração decimal.
Ex. 3/10, 9/100, 1625/1000, ...
Exercícios
Coloque V ou F em cada uma das seguintes sentenças:
a) 2/7 é uma fração própria ( v )
b) 2/2 é uma fração imprópria ( f )
c) 3/100 é uma fração decimal ( v )
d) 7/20 é uma fração decimal ( f )
e) Toda fração imprópria é aparente ( f )
f) 5/3 é uma fração imprópria ( v )
g) 3/1 é um número natural e fração aparente ( v )
h) Não existe fração com denominador zero ( v )
Frações Equivalentes
Duas ou mais frações que representam a mesma parte do inteiro são equivalentes.
Elas são muito úteis quando fazemos operações matemáticas entre frações (adição, subtração).
Exemplo de frações equivalentes.
1/2, 2/4 e 3/6
6/8 e 3/4
Entre elas podemos usar o sinal de semelhante (~) ou (=). Ex. 1/2 = 2/4, ...
Nas operações de adição ou subtração entre frações, o cálculo fica bem mais fácil quando conseguirmos deixá-las com o mesmo denominador, pois assim basta operarmos com os numeradores.
Vejamos a situação abaixo, na qual se pede que se determine a soma das frações que se seguem:
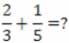
1º) Deve-se encontrar quais frações equivalentes às respectivas frações dadas acima que possuam os mesmos denominadores. Então, tem-se:
.jpg)
2º) Em seguida, substitui-se as frações dadas pelas suas respectivas equivalências e efetua-se a operação. Assim, tem-se:
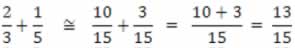
Exercícios
Fazer as operações abaixo entre as seguintes frações:
a) 2/3 + 3/5
Façamos o denominador comum entre 3 e 5 ou que achemos o mesmo denominador.
3.2=6, 3.3=9, 3.4=12, 3.5=15 →2/3 ~10/15 (multiplica-se numerador e denominador por 5)
5.2=10, 5.3=15 → 3/5~ 9/15 (multiplica-se numerador e denominador por 3)
Agora basta somar: 10/15 + 9/15 = 19/15 (somamos apenas os numeradores)
b) 4/3 - 2/7
Façamos com que as frações fiquem com o mesmo denominador ou o denominador comum entre 3 e 7.
3.2=6, 3.3=9, 3.4=12, 3.5=15, 3.6=18, 3.7=21 →4/3 ~28/21 (multiplicando por 7 ambos)
7.2=14, 7.3=21 →2/7~ 6/21 (multiplicando por 3 ambos)
Agora basta subtrair: 28/21 - 6/21 = 22/21 (subtrai-se apenas os numeradores).
Para saber mais sobre as operações entre frações, inclusive usando do MMC acesse o nosso conteúdo sobre Operações Fundamentais com Frações clicando aqui.
........................................................................................................................................................................................................................................................................................................................................................
Passo a passo da solução do teste de raciocínio matemático:
1. Que número fica diretamente acima de 167 na seguinte disposição de números?
12 3 4
5 6 7 8 9
10 11 12 13 14 15 16
- - - - - - - - -
- - - - - - - - - - -
Resposta: Observe que o último elemento das linhas é sempre um quadrado perfeito. Logo, a linha que contém a 167 termina com 169, e a anterior termina com 144, que está acima de 168. Então, o número acima é o 143.
2. Armando e Cleusa formam um casal de mentirosos. Armando mente às quartas, quintas e sextas-feiras, dizendo a verdade no resto da semana.
Cleusa mente aos domingos, segundas e terças-feiras, dizendo a verdade nos outros dias da semana.
Um certo dia ambos declararam: "Amanhã é dia de mentir". Qual o dia que foi feito essa declaração?
Resposta: Evidente que ambos só podem declarar esta frase na Terça-feira.
3. O algarismo das unidades do número N= 1x3x5x7x9x ... x999 é igual a:
Resposta: Observe que todos os números do produto, são ímpares, e além disso o produto de qualquer número ímpar por 5 termina com o algarismo 5. Logo, a opção correta é o 5.
4. Qual é a metade do dobro do dobro da metade de 2?
- A metade de 2 é 1;
- O dobro da metade de 2 é 2;
- O dobro do dobro da metade de 2 é 4;
- A metade do dobro do dobro da metade de 2 é 2;
- Então, a resposta é 2.
Filho é igual a A
Pai é igual a B
Mãe é igual a C
Avô é igual a D
Tio é igual a E
Pergunta-se: Qual é o A do B da C do A?
Resposta: Qual é o filho do pai da mãe do filho?
Resposta: É o tio que é igual a E.
...........................................................................................................................................................................................................................................................................................................................................................................................................................................................................
Para voltar para a postagem anterior, clique no botão voltar à esquerda ou acesse: Teste de Raciocínio Matemático, ou clique aqui!
 |
| A Matemática Aqui é Simples e Descomplicada! |











Adorei a forma abordada deste tema.
ResponderExcluirAbraços!
Agradecemos sua atenção e se gostou divulgue nosso blog para que outras pessoas também possam se beneficiar...
ExcluirAbraços!