Lados e Diagonais de um Polígono Convexo!

Como determinar o número de diagonais de um polígono convexo de n lados? 

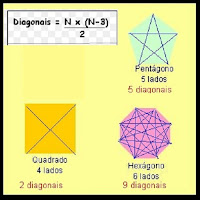
Fica muito fácil e simples determinar quantas diagonais tem um polígono convexo de N lados. Veja na figura ao lado, como é difícil contar manualmente quando se tratar de um polígono com muitos lados. No entanto, sabendo apenas o número dos lados do polígono convexo, podemos determinar o número das diagonais deste polígono. Neste estudo vamos relembrar e abordar este assunto tão importante da Geometria, de maneira bem simples e descomplicada. Antes porém, vamos relembrar algumas características e conceitos importantes dos polígonos:

A) Os polígonos recebem seus nomes, de acordo com o número de lados que eles possuem. Para relembrarmos o nome de alguns polígonos, verifique seus nomes consultando a tabela abaixo:

B) Num polígono qualquer, toda diagonal liga ou une dois de seus vértices conforme observamos na figura abaixo.

C) Note que parte apenas uma diagonal unindo dois dos vértices de cada polígono. 

Existe uma fórmula prática para encontrarmos as diagonais dos Polígonos?

O que queremos é encontrar uma forma para determinar a quantidade de diagonais sem termos que traçá-las em cada polígono. 

Observem que para um polígono de 4 lados, temos 1 diagonal partindo de um vértice; para um polígono de 5 lados, temos 2 diagonais partindo de um vértice; para um polígono de 6 lados temos 3 diagonais partindo de um vértice. Vejam que o número de diagonais que parte de um vértice é igual à quantidade de lados do polígono menos 3. 

Assim, podemos deduzir que para um polígono de N lados, teremos N−3 diagonais partindo de um vértice.

Então, podemos construir uma pequena tabela com os dados apresentados acima:

Nº lados do polígono	4	5	6	...	N
Nº de diagonais de cada vértice	1	2	3	...	N - 3

Como, sabemos que o número de diagonais de qualquer polígono é igual ao número de lados N do polígono, segue que teremos todas diagonais com extremidade nos N vértices dadas por: N⋅(N−3) diagonais

Mas, como cada diagonal tem suas extremidades ligando dois vértices, então cada diagonal fica contada duas vezes, por exemplo no quadrilátero, temos apenas 2 diagonais porque nos 4 vértices, cada diagonal liga 2 vértices. Então, para acharmos o número exato de diagonais de um polígono, basta dividirmos por dois, ou seja:

D = N(N−3)/2

Onde D representa o número de diagonais e N o número de lados de um polígono.

Agora, então já podemos realizar o cálculo das diagonais e podemos confeccionar outra tabela, com as diagonais de cada polígono como segue:

Nº lados do polígono	4	5	6	7	8	...	N
Nº de diagonais de cada polígono	2	5	9	14	20	...	N(N – 3)/2

Exercícios: 

1) Calcular o número de diagonais de um polígono de 250 lados?

Solução:

D = N(N−3)/2 = 250(250 − 3) / 2 = 250.247/2 = 30875

Logo, existe 30875 diagonais num polígono de 250 lados.

2) Qual é o polígono cujo número de diagonais é o quíntuplo do  número de lados?

Sabendo-se que D = 5N. Então, fazemos a substituição:N (N−3)/ 2 = 5N ⇒ N² −3N = 10N⇒N² − 13N = 0 ⇒ N(N−13) = 0

Então, concluímos que ou N=0 ou N=13. Mas, não faz sentido um polígono de 0 lados, logo tomamos N = 13 como solução. Assim, o polígono procurado é um tridecágono.

3) Sabendo-se que a diferença entre o número de diagonais de dois polígonos vale 85 e ainda que o número de lados de um é o triplo de número de lados do outro. Encontre estes polígonos?

Dizemos que D1 é o número de diagonais do polígono de NI lados e que D2 é o número de diagonais do polígono de N2 lados. Podemos retirar do problema as seguintes informações:

D1 - D2 = 85

N1 = 3N2

Então, podemos escrever que:

N1(N1-3)/2 - N2(N2-3)/2 = 85 →  N1(N1-3) - N2(N2-3) = 170 

(Substituindo N1 por 3N2) teremos:

3N2(3N2 - 3) - N2(N2 - 3) = 170 (fazendo N2=N)

9N² - 6N - N² - 3N = 170 → 8N² - 6N -170 = 0

N = 6 ± Ö 36 - 4.8(-170) / 16

N = 6 ± Ö 5476 / 16 = 6 ± 74 / 16 = 6  

N = 80/16 = 5  

Nota: A raiz negativa não nos interessa pois o que procuramos é a raiz positiva 5. Assim, fazemos:

Como: N1= 3N2 ⇒ N1 = 3⋅5=15

Concluímos então que os polígonos procurados são o pentágono e o pentadecágono.

CONCLUSÃO!

Gostaríamos de alertá-lo de que para aprender Matemática é necessário muita dedicação e resolução do maior número possível de problemas e exercícios. Então, recomendamos que pesquise outras questões e exercícios sobre o tema e se dedique em encontrar as soluções, que com certeza o aprendizado ficará mais otimizado.

Aproveite também para pesquisar em nosso Blog e acessar outros conteúdos importantes que são tratados na Geometria, procurando por este marcador neste site. 

Espero que tenham gostado da matéria e que a compartilhe com seus amigos ou pares. Para isso, recomendamos usar o atalho para as redes sociais que estão localizadas ao final da matéria, ou indicando nosso endereço aos mesmos.

Se ficou com dúvidas e quiser nosso parecer, use o espaço para comentários que vamos responder no menor prazo possível.

Aproveitamos também para convidá-lo a se cadastrar como seguidor do site e assim sempre receber nossas publicações inteiramente grátis e de forma automática.

Finalizando, agradecemos sua visita e apoio. Muito obrigado!

A Matemática Aqui é Simples e Descomplicada!