A Esfera!

A Importância de Conhecer e Estudar a Esfera?
Historicamente sabemos que os grandes cientistas e matemáticos de todos os tempos sempre estiveram pesquisando este importante conteúdo da geometria. O grande filósofo, físico e matemático francês chamado Blaise Pascal afirmou em um de seus pensamentos que: "O universo é uma esfera infinita, cujo centro está em toda parte e a circunferência em parte nenhuma". Outro grande nome da ciência que foi Aristóteles afirmou em uma de suas mais famosas frases que "o céu tem o formato da esfera, e que ele foi gerado pela rotação do círculo e que por isso seria o corpo mais belo e perfeito de todos". Assim, já podemos perceber a importância de estudar e aprender esse notável conteúdo da matemática. A forma da esfera está intrinsecamente ligada ao formato dos planetas e com o universo e reafirmamos que por isso, ele sempre despertou a curiosidade do mundo da física, astronomia e da matemática.

Muitos alunos nem imaginam mas quase todos eles já tiveram contato com a esfera, seja em sua intimidade e habilidade com uma bola de futebol, talvez brincando de bolinha de gude, ou até assistindo filmes ligados ao cosmos, tais como: Guerra nas Estrelas (Star Wars), Sphere (Esfera), quando visualizamos o formato arredondado de muitas estrelas e planetas nessas obras de ficção científica nos vídeos, tv e no cinema.

Elucidamos que a esfera é uma figura simétrica tridimensional que faz parte da geometria espacial. 

Contudo, definimos a esfera como um sólido geométrico obtido através da revolução da semicircunferência sobre um eixo, composto por uma superfície fechada na medida que todos os pontos estão equidistantes do centro.

Alguns exemplos de esfera são: os planetas, uma laranja, uma melancia, a bola de futebol, a maçã, dentre outros.

Componentes da Esfera

Superfície Esférica: É o conjunto de pontos do espaço no qual a distância do centro (O) é equivalente ao raio (R).

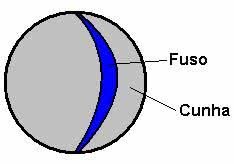
Cunha Esférica: É aquela parte da esfera obtida ao girar um semicírculo em torno de seu eixo.

Fuso Esférico: Dizemos que o fuso esférico corresponde à parte da superfície esférica que se obtém ao girar uma semicircunferência de um ângulo em torno de seu eixo.

Calota Esférica: É a parte da esfera  também chamada de semiesfera que é cortada por um plano.

Para que o leitor compreenda melhor os componentes da esfera, pedimos que analise os detalhes das figuras abaixo:

Fórmulas da Esfera

Destacamos abaixo as principais fórmulas que são usadas para calcular a área e o volume de uma esfera:

Área da Esfera

Para calcular a área da superfície esférica, utilizamos a fórmula:

Se = 4.п.r²

Onde:

Se= área da esfera

П (Pi): 3,14

r: raio

Volume da Esfera

Para calcular o volume da esfera, utilizamos a seguinte fórmula:

Ve = 4.п.r​³/3

Onde:

Ve: volume da esfera

П (Pi): 3,14

r: raio

Exercícios Resolvidos!

1. Qual a área da esfera de raio √5 m?

Para calcular a área da superfície esférica, utilizamos a expressão:

Se=4.п.r²

Se = 4. п. (√5)²

Se = 20п m²

Logo, a área dessa esfera de raio √5 m, vale: 20 п m².

2. Qual o volume da esfera de raio ³√6 cm?

Para calcular o volume da esfera, utiliza-se a expressão:

Ve = 4/3.п.r³

Ve = 4/3.п.(³√6)³

Ve = 24/3п.cm³

Ve = 8п.cm³

Portanto, o volume da esfera de raio ³√6 cm é de 8п.cm³.

3. Qual o raio da esfera cuja área é de 30 п m²?

Para achar o raio da esfera, devemos fazer a seguinte substituição:

Como: Se = 4.п.r² → 30 п m² = 4.п.r²

Então: 30m² = 4r² 

Logo: r² = 30/4 m² → r = √30/2 m

CONCLUSÃO!
Existe muitas considerações filosóficas ou não que são atribuídas a uma esfera, entre elas podemos destacar a esfera infinita que filosoficamente usando de uma metáfora seria uma maneira de se atribuir a alguém, algum fato ou até um relacionamento, que virou um circulo, comparado com uma esfera perfeita, para designar esse comportamento, como de um círculo vicioso e sem final. Nosso céu, por exemplo é definido por muitos pensadores e pesquisadores como sendo uma esfera infinita e até o Universo seria considerado como ela, cujo centro está em toda parte e a circunferência não estaria presente em parte alguma. Mas, são ilações que demandam polêmicas e controvérsias para que nosso leitor possa avaliar.

Entretanto, focando apenas no aprendizado desse importante conteúdo escolar que é a esfera e que deve ser estudado no Ensino Médio, aconselhamos que não fique preso somente aos exercícios resolvidos que divulgamos acima, mas que busque e pesquise outras formas de aprendizado, focando muitos outros problemas e questões que envolvam esse tema, pois o aprendizado verdadeiro e completo dessa disciplina somente se faz, exercitando e resolvendo o maior número de problemas e exercícios possíveis.

Se ficou alguma dúvida sobre o artigo, assim como na resolução dos problemas, deixe um comentário ao final do texto que teremos o maior prazer em elucidar, sempre no menor prazo possível.

Agora, se gostou desse artigo, faça o conhecimento circular, compartilhando esse texto nas redes sociais ou divulgando NOSSO ENDEREÇO a todos seus amigos e pares.

Finalizando, agradecemos a todos pela visita e apoio. Muito obrigado!

A Matemática Aqui é Simples e Descomplicada!