Divisão Proporcional

A divisão em partes proporcionais podem ser: DIRETAMENTE ou INVERSAMENTE proporcionais, ou seja:

Quando a divisão se der de forma diretamente proporcional, temos que, quanto menor o fator utilizado, menor será a parcela da divisão atribuída e quanto maior o fator utilizado, maior a parcela da divisão a ser atribuída.

 No caso de forma inversamente proporcional, temos que, quanto menor o fator utilizado, maior será o valor correspondente e vice-versa.

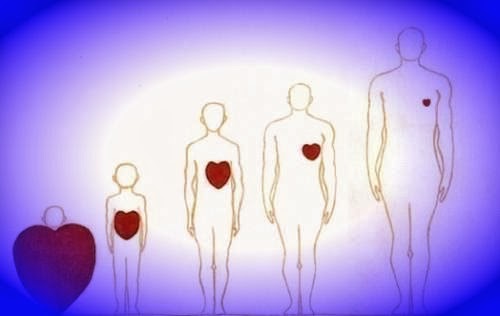
 No caso da figura acima, temos valores inversamente proporcionais se considerarmos coração e pessoa, pois a menor pessoa possui o maior coração e a maior possuir o menor coração.  Se considerarmos altura e pessoa, teremos valores diretamente proporcionais.

1) DIRETAMENTE PROPORCIONAL

 Podemos dividir em duas partes:

a) COM RELAÇÃO AO NÚMERO A SER DIVIDIDO
Se quisermos dividir o valor de R$ 13mil, proporcionalmente às idades de meus filhos de 3, 4 e 6 anos, queremos propor que o menor receberá menos e os maiores receberão mais, contudo em valores proporcionais às suas idades.  Então como fazer a divisão?

Devemos somar suas idades: 3+4+6 = 13

Aplicando uma regra de três simples: 

Idade do filho de 3 anos =x
13 ----------13.000,00             multipliquemos em cruz: 13.x=3.13000,00 --->13x=39000,00---->
3------------ x                          x=39000,00/13 ----> x=3.000,00
logo: meu filho de 3 anos receberá R$ 3.000,00

 idade do filho de 4 anos=y
13---------13000,00                multiplicando em cruz: 13y=4.13000,00 ---->13y=52000,00------>
4-----------y                            y=52.000,00/13 ------>y=4000,00       
logo, meu filho de 4 anos receberá R$ 4.000,00

 idade do filho de 6 anos=z
13--------13000,00                  analogamente, 13z=6.13000,00 ---> z=78000,00/13 -->z=6000,00
6-----------z 
logo, meu filho de 6 anos receberá: R$ 6.000,00, ou seja o dobro do filho de 3 anos.
Regra: O total a ser dividido está para a soma das partes proporcionais, assim como cada parte proporcional está para a parte que o representa.

Exercício resolvido.

Minha empresa recebeu um lucro de R$ 20mil, a ser dividido diretamente proporcionais, entre os meus empregados, os quais têm: 5, 10 e 20 anos de empresa.  Quanto deverá receber cada um?

 Somando as idades; 5+10+20= 35
Fazendo regra de três simples:

 Empregado de 5 anos=x
35-----------20000,00                    35x=5.20000,00--->x=100000,00/35 --->x=2.857,14
5-------------x

 Empregado de 10 anos=y
35-----------20000,00                    35y=10.20000,00--->y=200000,00/35 --->y=5.714,28
10-------------y

 Empregado de 20 anos=z
35-----------20000,00                    35z=20.20000,00--->z=400000,00/35 --->z=11.428,57
20-------------z
    
 b) COM RELAÇÃO ENTRE OS NÚMEROS PROPORCIONAIS.
Se uma pessoa dividiu uma fortuna entre 3 pessoas proporcionalmente às idades de 3, 5 e 8 anos e sabendo-se que primeira pessoa de 3 anos deverá receber 6.000,00 a menor que a segunda pessoa de 5 anos.  Então, quanto deverá ser o total da fortuna a ser dividida?  Ainda, quanto será o valor que cada uma delas receberá?

2ª pessoa = 5
1ª pessoa = 3
Diferença = 2 (5-3)

 Cálculo do valor da 2ª pessoa-x
Diferença: 2 ---------6.000,00
                   5----------x

 x.2 = 5.6000,00 ------>x= 30000,00/2 ---------->x = 15.000,00

 Cálculo do valor da 1ª pessoa=:y
Diferença: 2 ---------6.000,00
                   3----------y

 y.2 = 3.6000,00 ------> y = 18000,00/2 ---------->y= 9.000,00

 Cálculo do valor da 3ª pessoa=:z
Diferença: 2 ---------6.000,00
                   8----------z
   z.2 = 8.6000,00 ------> y = 48000,00/2 ---------->y= 24.000,00

Solução:  Valor da fortuna = 15mil+9mil+24mil = 48.000,00
                Valor de cada pessoa de 3, 5 e 8 anos respectivamente= {9mil, 15mil, 24mil}

Exercício c/ resposta.(qualquer dúvida, envie comentário que passamos a solução passo-a-passo).

Devo dividir um certo valor entre meus quatro colaboradores que têm: 2, 4, 7 e 10 anos de participação na empresa, sabendo-se que a diferença entre os mais velhos será de 10.000,00. 
Queremos saber:
a) Quanto será o valor total dividido?        b)Quanto receberá cada colaborador? 

Resposta: 
a) Valor total a ser dividido= 76.666,65
b) Colaboradores de 2,4,7 e 10 anos respectivamente receberão: {6.666,66, 13.333,33, 23.333,33, 33.333,00}

2) INVERSAMENTE PROPORCIONAL







Neste caso, quanto maior o valor ou a parte interessada na divisão, menor será o valor da parcela que caberá à mesma e vice-versa.
Usaremos neste caso, um artificio que será de inverter os termos do problema proposto,  para transformar assim o problema numa divisão diretamente proporcional, ou seja:

Exemplo: Divida o numero 2730 em partes inversamente proporcionais às frações: 3/5, 2/3 e 4/9.

 Invertendo os fatores e somando-se: 5/3+3/2+9/4 = (20+18+27)/12 = 65/12

Parte da Fração: 3/5 =x
65/12-----------2730
5/3--------------x

65/12 ---------2730
(5.4)/(3.4)-------x

65/12-----------2730        multipl.em cruz: 65x=20.2730 ----> x= 54600/65 --->x=840,00 
20/12-----------x

Parte da Fração: 2/3 =y
65/12-----------2730
3/2---------------y

65/12 ---------2730
(3.6)/(2.6)-------y

65/12-----------2730        multipl.em cruz: 65y=18.2730 ----> y= 49140/65 --->y=756,00 
18/12-----------y

Parte da Fração: 4/9 =z
65/12-----------2730
9/4--------------z

65/12 ---------2730
(9.3)/(4.3)-------z

65/12-----------2730        multipl.em cruz: 65z=27.2730 ----> z= 73710/65 --->z=1.134,00 
27/12-----------z

Resposta: Os valores inversamente proporcionais às frações: 3/5,2/3 e 4/9 serão respectivamente:{ 840,00: 756,00 e 1.134,00}

 Exercício com resposta.

 Dividir 4000 em partes inversamente proporcionais aos números: 3, 5 e 7?
(Dica: Os inversos de 3, 5 e 7 são: 1/3, 1/5 e 1/7)
Resposta: 1.971,83; 1.183,09 e 845,07
Observe que quanto menor a parte maior será a parcela dividida 
Teste "DP" com resposta na próxima postagem.

1) Dividir o número 7435 em partes inversamente proporcionais aos números: 4, 7 e 9.

2) Tenho três filhos com idades de 20, 14 e 10 anos.  Se quero repartir uma quantia de 100.000,00 em partes querendo que quanto menor a idade, maior a parcela a ser repartida proporcionalmente, quanto deverá receber cada um neste caso?

3) Tenho duas crianças que receberam 2.000,00 e 1.000,00 respectivamente diretamente proporcionais às suas idades.  Sabendo-se que a soma de suas idades vale 9, quais são as idades de cada um?  


 Bons Estudos





Sou o Professor Luiz Carlos Vivan, lecionei por vários anos a disciplina Matemática em várias escolas de ensino médio particulares e públicas do estado de São Paulo, autor dos artigos do Blog Recordando Matemática, sou especialista em Educação Matemática e também atuei no ramo bancário por 34 anos nas mais variadas funções administrativas e gerenciais. Nossa missão primordial com esse site educativo é divulgar e incentivar o estudo e o aprendizado dessa importante disciplina escolar. Aproveito para pedir que compartilhe e divulgue nossos artigos aos seu pares e amigos. Desde já agradecemos pela confiança e apoio.

Comentários

Postar um comentário

Ficou alguma dúvida sobre a postagem acima ou quer deixar uma sugestão?
Escreva seu comentário no espaço apropriado, seja para elogiar, criticar ou expor dúvidas, que publicaremos e responderemos o mais rápido possível.

Atenção: Serão excluídos os comentários contendo propagandas e também aqueles que faltem com o respeito e educação a qualquer usuário do Blog ou, os que venham induzir nosso leitor a acessar conteúdos impróprios e eticamente não recomendados. Desde já, agradecemos sua participação!




Postagens mais visitadas deste blog

Área de Figuras Planas!

Imagem
Por que é necessário saber calcular a área de figuras planas? Não temos dúvida nenhuma de que o conhecimento sobre a área das figuras planas é muito aplicado em nosso cotidiano, pois eles são utilizados nas construções, na Engenharia, Arquitetura, e em muitos outros campos do conhecimento que são essenciais para o conforto, design e desenvolvimento do homem. Sabemos que a Geometria, de um modo geral, sempre contribuiu muito para a evolução humana, sem nos esquecermos das suas aplicações na natureza e até no universo. Veja que ela esteve presente nas construções antigas das pirâmides do Egito, e também na natureza, como por exemplo, nas colmeias das abelhas, onde são encontrados as figuras de muitos hexágonos e cujos estudos nos indicam que esta forma foi adotada pelas abelhas porque pode abrigar a maior quantidade de mel que elas produzem. No universo, veja que os movimentos dos planetas deixam rastros em suas órbitas, sendo que seus caminhos são da forma arredondada, formando ...
Read more »

Duas Retas Paralelas se Encontram no Infinito?

Imagem
Você Acha que Duas Retas Paralelas se Encontram no Infinito? Esta pergunta é semelhante à seguinte: Será que duas linhas ou retas paralelas se encontram no infinito? Essa resposta, depende do tipo de geometria que você estiver considerando no momento da análise deste assunto. Sabemos que a solução pode ser dada de duas maneiras distintas que depende do tipo de Geometria que você se basear. Enfatizamos que, talvez a geometria projetiva apresente uma resposta afirmativa condizente e de modo muito satisfatório. No entanto, pela visão da geometria euclidiana, considerando-se que estas retas  ou duas linhas paralelas são definidas como duas linhas que nunca se cruzam, quando consideramos apenas o plano finito. Então, a resposta obtida seria, segundo Euclides  negativa. Ou seja, considerando-se esta corrente de pensamento, linhas paralelas nunca vão se cruzar. No entanto, quando o  plano euclidiano , chamado também de plano finito, for ampliado ou alargado, adicionando...
Read more »

Calculo da Área de um Triângulo Qualquer

Imagem
Ângulos e Triângulos Ângulos A unidade de medida de um ângulo chama-se grau, cujo símbolo é:  (º) e os seus submúltiplos são o mínuto,  (') e o segundo, (").   Exemplo: 1º = 60 ' e 1' = 60" logo: 1º = 3600"  Classificação dos Ângulos Eles podem ser: Agudos - Quando medem menos que 90º Obtuso - Quando medem mais que 90º Reto - Quando medem exatamente 90º Raso - Quando valem exatamente 0º ou 180º Bissetriz de um ângulo - É a semi-reta que tem origem no vértice de um angulo principal e o divide em dois ângulos iguais. Triângulos Sabemos que eles têm 3 lados e 3 ângulos internos que somam 180º. Classificação dos Triângulos: Se dá: De acordo o medida de seus lados : Equilátero - Aquele que possui os 3 lados iguais. Escaleno = Têm os 3 lados diferentes. Isósceles - Têm dois lados iguais. Ou de acordo com a medida de seus ângulos: Equilátero - Têm os 3 ângulos congruentes que valem 60º Isósceles - Têm dois ângulos congruentes e outro diferente, sal...
Read more »